量子力学中虚数的数学形式和物理意义|复数|实数|张量|数学|薛定谔|虚数|量子力学

前言：本文严格来说只有首尾部分算是科普内容，中间部分对多数人来说有一定难度，请读者自己酌情选择章节阅读。

概述：

在数学中，我们常见的实数是包括正负数在内的一切自然数和小数，而与之对应的是虚数，我们用符号i来表示。

在量子力学中经常出现虚数，它在其中扮演什么角色？有什么意义？这是一直以来困扰大家的一个问题。通过本文我们简单了解一下虚数的数学概念，以及在量子力学中的运用。

我们对虚数最直观的认识是：虚数是虚拟的、不是真实存在的

1-虚数的数学基础

1-1.虚数的基本概念

虚数i是17世纪的数学家笛卡尔创立的，认为这是不真实存在的数字。像x²+1=0这样的二次方程，在实数范围内没有解，于是就采用了虚数i，并定义i²=-1。

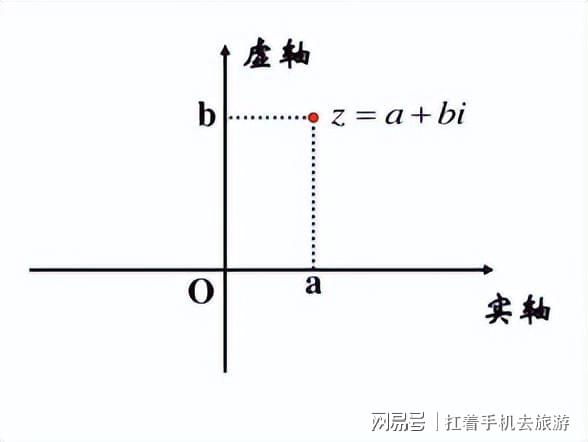
图1

到18世纪，数学家欧拉系统地使用了虚数i，用数偶(a、b)来表示复数a+bi，其中a为实部b为虚部，且均为是实数，且b≠0（见图1）。

复数a+bi的实部a对应平面上的横轴（实轴），虚部b对应平面上的纵轴（虚轴），这样复数a+bi即可与平面坐标内的点(a,b)相对应。

1-2.虚数i的几何意义

为理解虚数的意义，用以下平面几何的例子做解释：

图2

如存在一个数轴，上面有两个反向点，数字为+1和-1，中间是原点0（见图2）。

图3

将数轴的+1，绕原点逆时针旋转180度，+1就会变成-1（见图3）。

图4

分解动作，相当于两次逆时针旋转90度（见图4），设“每次逆时针旋转90度”= A，注意A不是一个普通变量，而是一个过程向量，代表了旋转过程，则：

(+1)*A*A = -1

化简，得

A² = -1

令A=i，于是

i² = -1

由此可见：虚数i就是逆时针旋转90度，i不是一个数，而是一个旋转量；一个数乘以i，就是将复平面中表示该数的向量逆时针旋转90度。

1-3.虚数i的简单运算

虚数i不能和任何实数直接做加减法，比如8和2i相加只能写作8+2i，因为二者意义完全不同。

但是虚数之间可以做加减法：

5i+3i = 8i

5i-3i = 2i

虚数之间可以做乘法：

i*i = i² = -1

n为自然数时，符号^为幂次方（下同），则：

i^4n = 1

i^(4n+1) = i

i^(4n+2) = -1

i^(4n+3) = -i

2-虚数与欧拉公式

2-1.改变虚数意义的伟大公式

数学家欧拉进一步发展了虚数，在1752年，他写出了这个世界上最完美的数学式，即欧拉公式（见图5）：

图5：欧拉公式

因输入法原因，在本文中书写如下：

e^iθi = cosθ+ isinθ（符号^表示幂次方，下同）

i是虚数单位；e是自然常数，e≈ 2.71828…；θ是实数（表示角度，以弧度为单位）。当θ=π时，公式写作：

e^(πi) + 1 = 0

它将数学里最重要的几个数字联系到了一起，两个超越数：自然常数e，圆周率π；虚数单位i和自然数0、1。数学家们评价这个公式是“上帝创造的公式”，它将三角函数与复指数函数巧妙地关联了起来，在几何上的解释如下：

图6：复平面中的虚轴

在复平面的坐标系中，横轴为实数轴，纵轴为虚数轴，因三角函数

sin²θ+ cos²θ = 1 = - i²

则欧拉公式产生了一个半径为1的圆（见图6）。

图7：复平面中的虚数

那么圆上任意一点，在实轴上投影的分量为cosθ，在虚轴上的分量为sinθ（见图7），这就是欧拉公式几何上的意义。

2-2.平面简谐波函数基础

图8：平面简谐波

简谐振动的传播所形成的波，称为简谐波（见图8），简谐波是最简单、最基本的波，一切复杂的波都可看成由多个简谐振动的传播所构成的波合成的。

图9：平面简谐波的参数

比如X轴上距原点O为x的任意一点P的振动情况（见图9），因为振动是从O点传过来的，所以P点振动的相位将落后于O点。

λ为波长，表示同一波线上两个相位差为2π的点之间的距离；T为周期，表示一个完整的波通过波线上某点所需的时间；f为频率，表示为单位时间内通过波线上某点的完整波的数目；u为波速，因为在一个周期内波前进一个波长的距离，所以波速u=λ/T=λv；ω为角频率，表示单位时间内变化的相角弧度值，ω=2πf；k为波数，表示每单位长度内的整波数量，k=2π/λ。

则原点O点处的质点振动为：

X(t) = Acos[ωt+φ0]

φ0表示初相位，则P点处的质点振动写作：

X(t) = Acos[ω(t-x/u)+φ0]

因ω=2π/T，u=λ/T，k=2π/λ，可简化为函数：

f(x,t) = Acos[(ωt-kx)+φ]

2-3.虚数与波函数

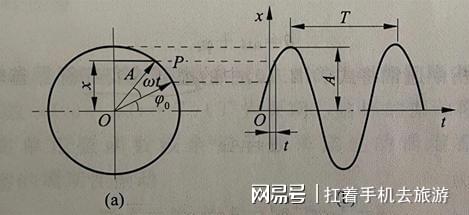
图10：三角函数与复函数的投影关系

将上述三角函数的波函数，映射到复平面中（见图10），可得：

X(t) = A(cosθ+isinθ)

其中θ=ωt+φ0，复矢量的虚部与实部均为简谐函数，实部Re=Acosθ，虚部Im=Asinθ。为方便起见，在振动分析中通常将式中的虚部或实部符号省略，代入欧拉公式，则距离原点为x的点P点的简谐振动的复数表达式可以写成（见图11）：

图11：简谐振动的复数表达式

k为波数，ω为角频率，x为位置，t为时间，图11函数还可写作：

f(x,t)= Ae^i(kx-ωt+φ)

对于图10的原点O，因k=0，θ=ωt+φ0，简谐振动的极简表达式就写成：

f(x,t) = Ae^iθ= Ae^iωt

自此，我们完成了用复数来表示平面简谐波。

进入物理部分之前总结一下，量子力学中的简谐波函数，带虚数的复指数形式，等同于三角函数形式（见图12）：

图12：后面的量子力学会反复出现复指数函数，请记住这组等效公式

3-虚数与应用物理：

在应用物理学中，虚数用于描述振动波和解析函数。

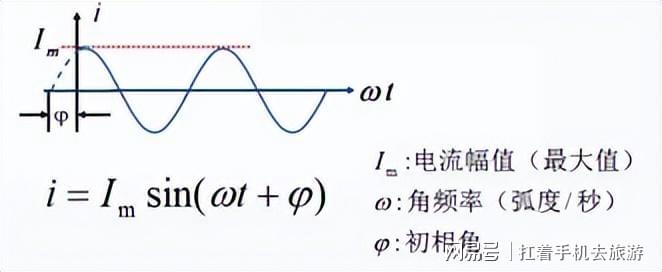
图13：三角函数表示电流

比如欧拉公式在交流电路分析中，电压和电流（见图13）通常是正弦函数形式：

V(t) = Vm sin(ωt)

I(t) = Im sin(ωt+φ)

其中，Vm和Im是幅值、ω是角频率、φ是相位差。在实际电路中，电压和电流之间可能存在电阻、电感和电容等元件的影响，因此需要进行复数运算才能得到准确的结果。

通过欧拉公式，我们可以将正弦函数表示为复指数函数的形式：

e^(iωt) = cos(ωt) + isin(ωt)

这种表示方式方便进行复数运算和分析，例如计算电压和电流的相位差、复功率等。

图14：傅里叶变换

又如欧拉公式在数字信号处理中，往往需要进行傅里叶变换（即函数与三角函数的变换，见图14）来将时域信号转换为频域信号。其中，F(ω)表示频域信号、f(t)表示时域信号，这种表示方式方便进行复数运算和分析。

但是虚数与应用物理的联系，并不是本文重点，下面开始着重介绍虚数与量子力学的联系。

4-虚数在量子力学的运用：

4-1.虚数与薛定谔方程，还有那只猫

图15：薛定谔（1887 -1961），奥地利物理学家，1933年诺贝尔物理奖获得者

上图（见图15）就是大名鼎鼎的薛定谔方程，用于描述粒子波动中时间、位置、能量、质量的函数关系。但这是缩并的定态方程，其三维形式如下：

ih∂ψ/∂t = V(x,y,z)ψ - h²(∂²ψ/∂x²+∂²ψ/∂y²+∂²ψ/∂z²) /2m

这是个二阶偏微分方程，其中的ψ为粒子的波函数，h是约化普朗克常数，m为粒子质量，t为时间，∂²ψ/∂x²、∂²ψ/∂y²、∂²ψ/∂z是波函数对三维空间求偏导， V(x,y,z）就是粒子的势能。

方程左边的i，就是我们最关心的虚数。对方程求解后i是无法消去的，薛定谔自己也无法解释其意义，反倒是物理学家玻恩做出了合理解释，对方程左边取平方则有：

|iψ²|=ψ²

图16：电子绕核运动形成的电子云

对薛定谔方程波函数和虚数取平方的绝对值，即|iψ²|=ψ²表示了粒子在空间某处位置出现的概率，这就是量子力学中概率云的概念，即粒子具有波粒二象性，其波动位置是无法准确确定的，只能以概率统计的方法确定其出现在某一位置(见图16)。

图17：著名的薛定谔的猫

于是，薛定谔的那只猫(见图17)是死是活，我们解释为：密封在盒子内的猫，其生死状态（暗寓为粒子的位置状态），不是确定的，生或死都存在一定的概率。

虽然在数学上暂时解决了薛定谔方程中虚数的问题，但是我们最关心的虚数i的物理意义，还是没有解决，接力棒交到了下一位大师—狄拉克的手中。

4-2.虚数与狄拉克方程

图18：保罗·狄拉克（1902—1984），英国物理学家，1933年诺贝尔物理奖获得者

1928年，狄拉克(见图18)把相对论引进了量子力学，建立了著名的狄拉克方程（见图19），是用来描述带电粒子在电磁场中的运动轨迹和相互作用的理论工具，它规定了电子和反电子以及它们的自旋方向。

图19：狄拉克方程是张量形式

狄拉克方程是从薛定谔方程推导出来的，区别是：薛定谔方程适用于低速粒子；狄拉克方程结合了相对论，描述了接近光速的费米子运动，这从方程中的光速c就能看出来。

h是约化普朗克常数；ψ为波函数；∂_u表示ψ对四维时空求偏导，u =0,1,2,3；m为粒子质量；γ^u为狄拉克矩阵(见图20)。

图20：狄拉克矩阵

γ^u作为一种特殊张量，u=0,1,2,3，为包含了虚数i的4×4的矩阵形式，表示相对论效应下的四维时空中，是以16个狄拉克矩阵作为基矢构建的线性空间中的代数结构，在这个空间中，通过定义‌反对易关系来定义狄拉克矩阵之间的乘法关系。

图21：γ^u和∂_u两个矩阵的并乘

矩阵γ^u和∂_u相乘后(见图21)，虚数无法消去。

显然，狄拉克方程中的最左边虚数i，是为了对上面矩阵中的虚数i消项，而在数学上进行的一个变通，这是薛定谔方程的延续，依旧没有给出物理意义上的解释，于是把问题留给了后来的量子电动力学（简称QED）。

4-3.虚数与量子电动力学（QED）

从上世纪二十到五十年代，狄拉克、海森伯、泡利、费曼（见图22）等物理大师奠定了量子电动力学的理论基础，并逐渐发展成熟。量子电动力学研究的对象是电磁相互作用的量子性质（即光子的发射和吸收）、带电粒子的产生和湮没、带电粒子间的散射、带电粒子与光子间的散射等等。在QED的经典理论中，更是随处充斥着虚数i。

图22：理查德·费曼（1918—1988），因QED理论的卓越成就，获得1965年诺贝尔物理学奖

4-3-1.QED中的光子散射

量子电动力学中，光的散射即入射光子被原子散射到新方向的现象，可以把这个过程看作原子吸收入射光子并发射新的光子（见图23）。

图23：光子散射的各种方式

假设光子从状态k到状态l，那么这两个光子的矢势可以这样表示（见图24）：

图24：光子不同状态的矢势公式

i为虚数，ω为角频率，e为自然常数，h为普朗克常数，e1、e2为电子电荷量，k为波数，x为光子位置，t为时间。

注意：参见图12公式，复指数函数等同于三角函数，不是真正意义上的虚数。

那么光子跃迁中的散射截面（即散射概率）为（见图25）：

图25：光子散射截面计算公式

E为能量，p为动量，c为光速，m为电子质量；dΩ为曲面微分，代表光子跃迁所在范围；δ为克罗内克张量符号（一种0或1的特殊态张量）；n=1,2,3…n，表示光子从状态k到状态l的全部路径（为无数个）；其余符号含义同上。该方程没有出现虚数，它表示了光子被原子散射所经过路径的各种概率。

4-3-2.QED中的传播子

在量子电动力学中，传播子并不是一种粒子，而是表示粒子从一点移动到另一点的概率幅，由所有可能轨迹的概率幅叠加而成（见图26）。

图26：传播子可能的运行轨迹以概率表示

一般使用路径积分求解传播子，电子从能量E1跑到E2，并且微扰势正比于exp(iωt)，则这个微扰势带来正能ω，任意散射幅正比于（见图27）：

图27：自由粒子散射幅计算

其中i为虚数；其中exp表示以常数e为底的指数函数，其表达式为exp(x)=e^x；E为能量；ω为角频率；t为时间。

那么自由电子的传播子可用K(2,1)表示为（见图28）：

图28：自由粒子的传播子公式

图27、28公式中的虚数i是复指数函数，是实数而不是虚数（见图12）。

K(2,1)在这里实际上是粒子的态函数；ω为角频率；p为动量；m为质量；x为位置。该方程表示了粒子跃迁过程中，动量与路径的概率关系。

4-3-3.QED中的费曼图和正负电子湮灭

为了研究单光子或多光子的发射和吸收、电子的产生和湮没、电子间的散射、电子与光子间的散射等，费曼图（见图29）是必不可少的工具。

图29：这就是著名的费曼图，实线表示电子，波浪线表示光子

QED还引入了虚粒子的概念，将携带力的虚粒子作为微粒之间进行相互作用的媒介，虚粒子是短暂出现的具有不允许的能量或动量的粒子。以正负电子相遇湮灭成光子的散射过程为例（见图30）：

图30：正负电子相遇湮灭成两个光子的表达式

正负电子湮灭成光子的散射过程，可以通过不止一张费曼图来表示。我们用p1表示负电子、p2表示正电子，q1、q2表示光子，常见的表示方式就有以下两种（见图31、33）。

图31：散射方式1

第一种相互作用的矩阵元为（见图32）：

图32：矩阵元1

其中i为虚数；u为电子旋量；€为置换张量(一种顺时针或逆时针旋转矩阵的方式来置换元素)；其余符号含义同上。

图33：散射方式2

第二种相互作用的矩阵元为（见图34）：

图34：矩阵元2

粒子2为正电子，取正电子速度为p+/E+，散射截面为（见图35）：

图35：电子的散射截面公式

i为虚数；e1、e2为电子电荷量；dΩ为曲面微分；ω为角频率；p为动量；E为能量；m为质量；x为位置。该方程表示了正负电子相遇并湮灭过程中，动量与粒子运动路径的概率关系。

为了消除图32、34公式中矩阵元的i，图35公式中从矩阵元换算过来的动量P求模值，只保留两个矩阵元中复数的实数部分，从而变成全实数运算式。

4-3-4.QED中的虚数i和虚光子

与薛定谔方程、狄拉克方程中直接出现虚数i参与计算不同，QED章节4-3-1~3的光子散射、电子跃迁、正负电子湮灭，以复指数形式出现的波函数中虚数i实际上就是实数函数，这是为了公式简洁和方便计算（见图12）。

虽然图35公式在计算电子湮灭成光子的概率问题时，利用数学技巧消去了i，但是中间过程出现虚数i是不能省略的，描述见下。

QED最基本的观点是，电磁力的传递是通过交换虚光子进行的，这种交换可以有很多种不同的方式。比如两个电子之间最简单的传递方式是：第一个电子放出虚光子被第二个吸收；第二个电子收到虚光子后也放出一个虚光子被第一个电子吸收，如此继续下去。稍微复杂一点的两个电子交换虚光子过程是：一个电子发射出一个虚光子后，那虚光子又可以变成一对电子和反电子，这个正反电子对可以随后一起湮灭为虚光子，也可以由其中的那个反电子与原先的一个电子一起湮灭，使得结果看起来像是原先的电子运动到了新产生的那个电子的位置；更复杂的，产生出来的正反电子对还可以进一步发射虚光子，虚光子可以再变成正反电子对……而所有这些复杂的过程，最终表现为两个电子之间的相互作用。

图36：传递电磁波的光子，是一种虚粒子

由此可见，虚光子（见图36）就是能量交换的媒介子，电子吸收或辐射能量就是以虚光子作为能量交换的砝码。

我们暂时得出以下结论，QED中虚数i代表的物理意义：是光子与电子、正电子与负电子之间相互作用中虚光子的产生和湮灭过程，这是一个作用过程，而不是虚光子本身，比如虚光子以光速作用的产生和湮灭。

4-4.QCD和规范场中的虚数i和虚粒子

图37：散射截面原子核内部的质子和中子，都是由三个夸克构成的

4-4-1.QCD即量子色动力学，研究的是原子核内部的强核力。胶子在三个夸克之间以光速来回运动，传递强核力（见图37），其中最重要的，表示其作用强度的色流方程如下（见图38）：

图38：量子色动力学中的色流方程，二阶张量形式

色流J_u^α是一个二阶混合张量，表示不同色荷的夸克间的作用强度，类似于QED中电子所带的电流，其中的指标u=0,1,2,3表示四维时空；指标α=0,1,2…8为李群指标，表示夸克的味（夸克之间8种胶子的作用）；λ为与之对应的8个盖尔曼矩阵（见图40）；ψ^ix为夸克场，ψ^-ix为胶子场；g为耦合常数；γ_u为狄拉克矩阵（见图19）。

注意方程中的i不是虚数符号而是张量指标，i=1,2,3表示夸克的三种色荷（夸克的自由度）；符号j是张量指标，是由李群指标α和色荷指标i所决定的李群结构常数中的指标。

因为λ和γ_u都是含有虚数的矩阵，对项并乘中虚数消项成为实数。而求和符号∑则意味着夸克之间存在的渐进自由，是非线性的过程。

QCD中胶子本身也带色量子数，夸克场ψ^ix所带的一部分色流J并不守恒，只有它与胶子场ψ^-ix所带色流之和才是守恒的，即方程中的色流J_u^α也包含了胶子场的作用。与QED类似，虚数i在QCD中的意义是：胶子作为虚粒子，在夸克之间的运动并交换能量的过程，就表示为虚数i。

4-4-2.最后来看规范场论，其l代表方程就是杨—米尔斯方程（见图39）：

图39：杨—米尔斯方程

由于我之前的《张量数学是如何描述爱因斯坦场方程和杨—米尔斯方程的》一文中，已经作了详解，此处不再细说。

杨—米尔斯方程看似没有虚数i出现，方程中的张量指标i（注意这是张量分项而不是虚数）就是选择基底矩阵的SU(N)群（见图40）：

图40：杨-米尔斯方程中选择基底的矩阵

矩阵中就出现了虚数i，为了消去虚数，图39公式中的作用量F_uv的平方并取负，就得到实数的拉格朗日量。

规范场论本身就是以麦克斯韦方程、QED、电弱V-A理论等为基础发展而来的，并成功的预测了QCD和GSW规范场（电弱统一理论，非常复杂，我们下一次单独讲述），构建了标准物理模型。可见规范场论与QCD和QED具备一样的数学形式和物理意义。

5-虚数i在量子力学中的本质

5-1.虚数式的数学解释

虚数i从诞生之初就不是一个数字，而是表示一个物理量。

结合前面的全部内容，量子力学中以Hi形式出现的复数，其中：i为虚数，表示的不是数字而是过程（见图41）；H为变量、数组、矩阵、张量、函数等任意实数形式，表示的是粒子的动量、能量、速度、质量…等物理量。

图41：量子力学中，虚数可以理解为一个虚拟的过程，即无法观测的事实

那么Hi表示的就是上述物理量的转换过程。究竟是什么具体过程，见后面详解。

5-2.虚数i的本质一

量子力学中，使用了含虚数的复数函数和单独出现的虚数i来描述粒子波（二者的区别上面已经反复说明过）。薛定谔方程、狄拉克方程、QED、QCD、规范场论的公式均使用了虚数i，公式中只要看到虚数i就意味着是对粒子波动性质的描述，这反映的是量子力学中粒子运动的不可预测性，即不确定性原理。

为了求解动能、动量、矢势、位置、作用强度、时间、概率、态密度、截面…这些实数物理量（如果为虚数，将是毫无意义的；但是可以能量可以为负数，比如部分虚粒子就可以携带负能量，以抵消多出来的一部分能量），物理学家采用了平方、取模值、并乘虚数矩阵、张量转置等方法最终消去了虚数，那为什么还要保持这种虚数表达方式呢？仅仅是为了波函数的简捷运算，还是为了形式？答案是这些方程必须保留虚数，因为物理方程的意义不是仅仅寻求结果，而是推导物理过程，虚数在这些方程式中体现的就是上面所说的粒子运动不确定性。

图42：虚粒子在宇宙中无处不在，并随时产生和湮灭

于是我们得出量子力学方程中的虚数第一个意义：虚数表示了费米子之间交换玻色子的过程，即i表示的不是粒子，是粒子之间交换能量的过程，也是虚粒子生成和湮灭的过程（见图42）。

5-3.虚数i的本质二

虚粒子定义为真实存在但不可直接观察的粒子，我之前的《粒子、反粒子和虚粒子》一文中有详细解释。

结合文章1-2章节对虚数的几何定义：i不是一个数，而是一个旋转量。我们还能得出虚数的其它意义，即虚数是一种张量或数组的旋转，或者说是参考系的改变，那么其物理上是一种不可观测的变化过程，只是我们从自己所在的宇宙无法观察到，要是在另一个平行宇宙呢，是否能够观测到这种过程？这实际上是从量子向宏观宇宙的过渡，也是一种思维方式的转变。