精确性与确定性,是数学陈述与生俱来的鲜明标志,这一点在学界乃至大众认知中都无可争议。从基础的算术运算到复杂的拓扑几何,每一个数学结论的推导都遵循严格的逻辑法则,每一个数学命题的真伪都有着明确的判断标准。

然而,当我们跳出具体的数学问题,追问“数学本身是人类的发明还是对客观存在的发现”这一根本性问题时,原本统一的认知便瞬间分裂为针锋相对的阵营。这种充满思辨性的争议,本是哲学领域探讨存在与认知、主观与客观关系的经典议题,却因数学这一极具客观性的学科而变得更加复杂多元。事实上,“数学是发明还是发现”绝非非此即彼的简单选择题,而是一个横跨哲学、数学、认知科学与人类学的跨学科课题,它不仅关乎我们对数学本质的理解,更牵涉到人类认知边界、文明发展路径等深层命题,显然无法仅凭数学学科自身的逻辑体系直接给出答案。
要理清这一争议,首先需要明确“发明”与“发现”的核心差异。从概念内涵来看,“发现”的本质是对已有存在的探寻与揭示,它暗示着在人类心智之外,存在着一个真实的、独立的“数学世界”——无论是具象的物理宇宙背后的规律,还是抽象的超验领域中的法则,数学的任务只是像探险家测绘未知疆域一样,将这些早已存在的规律挖掘出来。而“发明”则聚焦于人类心智的创造性活动,它强调数学是人类为了理解世界、解决问题而构建的思维工具,无论是具体的数学概念、运算规则,还是完整的理论体系,都是人类主观建构的产物,而非对客观存在的直接映射。

两种观点的分歧,本质上是对“数学对象的本体论地位”的不同认知:数学对象是独立于人类认知的客观存在,还是依赖于人类思维的主观构造?正是这一核心分歧,衍生出了绵延至今的学术争论。
在这场争论中,学界形成了两大主流阵营,同时也存在一种调和性的观点。一部分学者秉持柏拉图主义立场,坚定地认为数学是“发现”;另一部分学者则站在形式主义的角度,主张数学是“发明”。此外,还有一种更具包容性的观点逐渐获得更多认同:“数学是发明还是发现”本身就是一个伪命题,因为数学兼具发明与发现的双重属性——通常情况下,数学概念是人类的发明,而基于这些概念推导得出的定理与规律,则是对概念间内在关联的发现。为了更清晰地阐释这一观点,我们将在后续的论述中,以欧几里得提出的黄金分割率为核心例证,深入剖析数学如何在人类的创造性建构与客观规律的探寻中实现统一。
观点一:数学是发现——对客观数学世界的探寻
柏拉图主义是“数学是发现”这一观点的哲学根基。柏拉图认为,在可感知的物理世界之外,存在着一个永恒的、完美的“理念世界”,而数学对象正是这一理念世界的重要组成部分。人类对数学的研究,本质上就是通过理性思维去洞察和发现理念世界中早已存在的数学规律。在现代数学界,许多顶尖学者都传承了这一思想,法国数学家阿兰·孔涅(Alain Connes)便是其中的典型代表。孔涅是数学界的传奇人物,先后斩获了菲尔兹奖(1982年)与克拉夫德奖(2001年)这两项数学领域的最高荣誉,其学术成就涵盖算子代数、非交换几何等多个前沿领域。基于自身深厚的数学研究经验,孔涅清晰地表达了自己的柏拉图主义立场。
孔涅认为,质数所构成的数学世界,远比我们身处的物质世界更加稳定、更加真实。
在他看来,数学家的工作与探险家的探险活动有着异曲同工之妙:探险家通过实地考察发现未知的山川河流、动植物种,而数学家则通过逻辑推理与理性思考,发现数学世界中早已存在的基本事实与内在关联。为了佐证这一观点,孔涅以质数的研究为例:通过简单的枚举与计算,我们可以直观地感受到质数序列似乎没有尽头,但这只是一种感性认知;而数学家的核心任务,便是通过严格的逻辑论证,证明“存在无穷多个质数”这一客观事实——这一结论早在古希腊时期就由欧几里得提出并完成证明。
孔涅特别强调,这一论证过程具有无可辩驳的客观性:即便有一天有人宣称发现了“最大的质数”,我们也能依据已有的数学逻辑轻松证明这一说法的谬误。在孔涅眼中,这种不依赖于人类主观意志、具有绝对确定性的数学现实,与物理世界中那些可观测、可验证的客观现象并无本质区别,它们都是独立于人类认知之外的真实存在。
知名数学科普作家马丁·加德纳(Martin Gardner)也坚定地支持“数学是发现”的观点。加德纳一生撰写了数十部数学科普著作,以通俗易懂的语言将复杂的数学知识传递给大众,其作品影响了一代又一代的数学爱好者与研究者。
在加德纳看来,数与数学规律的存在具有绝对的独立性,无论人类是否能够认识到它们,它们都客观地存在于世界之中。为了形象地阐释这一观点,加德纳曾提出过一个风趣的设想:“如果森林中有2只恐龙与另外2只恐龙相遇,不管周围是否有人类在观察,那儿都会有4只恐龙。但是,愚蠢的熊却不会知道。”这个看似简单的例子,精准地揭示了数学规律的客观性:“2+2=4”这一数学事实,并不因人类的观测与否而改变,也不依赖于人类是否发明了“加法”这一运算规则——它是宇宙间固有的客观关联,人类的工作只是发现并描述这种关联。
加德纳进一步指出,当人类通过理性思维理解了某个数学概念后,就必然会面临一些无可争议的客观事实,这些事实是概念本身所蕴含的内在属性,与人类的主观认知方式无关。
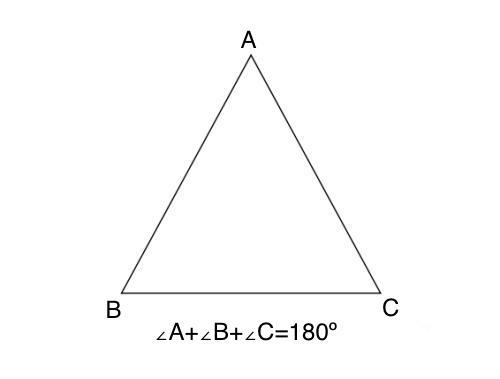
例如,当我们理解了“自然数”的概念后,就会自然地发现“任意两个自然数的和仍然是自然数”“存在唯一的最小自然数1”等客观规律;当我们掌握了“三角形”的定义后,“三角形内角和为180度”“任意两边之和大于第三边”等定理便成为了必然的客观事实。这些规律与定理并非人类的主观创造,而是数学概念自身所固有的属性,人类的理性思维只是发现这些属性的工具。这种观点背后蕴含着一种深刻的信念:数学是对客观世界本质规律的抽象反映,它的客观性决定了它只能被发现,而不能被发明。
观点二:数学是发明——人类心智的创造性建构
尽管柏拉图主义的观点具有强大的说服力,但并非所有学者都认同这一立场。许多数学家、哲学家与认知科学家从人类认知的局限性、文明发展的多样性等角度出发,提出了相反的观点:数学是人类心智的创造性发明,是人类为了适应环境、解决问题而构建的思维工具。英国数学家迈克尔·阿蒂亚爵士(Michael Atiyah)便是这一观点的重要代表。阿蒂亚是20世纪最伟大的数学家之一,曾获得菲尔兹奖(1966年)与阿贝尔奖(2004年),其研究成果横跨代数几何、拓扑学、数学物理等多个领域,对现代数学的发展产生了深远影响。在为孔涅的著作撰写评论时,阿蒂亚表达了自己对柏拉图主义的质疑。
阿蒂亚承认,每一位数学家在研究过程中,都会或多或少地感受到整数、圆等数学对象的“真实性”,柏拉图主义的观点确实具有很强的吸引力。但他同时指出,这种“真实性”并非来自于独立的理念世界,而是源于人类对物理世界的感知与抽象。阿蒂亚提出了一个极具启发性的设想:如果宇宙是一维的,或者是离散的,那么几何学这一数学分支是否还能孕育发展?答案显然是否定的。
几何学的产生,源于人类对二维、三维空间的感知与认知——人类生活在三维空间中,能够直观地感受到平面、立体等几何形态,正是这种对物理空间的体验,为几何学的发明提供了基础。同样,整数与计数概念的产生,也与人类的生活体验密切相关:人类在长期的生产生活中,需要对物品的数量进行统计,才逐渐发明了计数的方法与整数的概念。
为了进一步说明数学的发明属性,阿蒂亚还构想了一个极端的场景:假如文明并非诞生于人类之中,而是诞生于潜藏在太平洋深处、独居且与世隔绝的水母之中,那么它们所构建的“数学”将会是什么样子?水母没有个体的体验,只能通过身体感知周围水流的运动、温度与压力的变化,在这样的生存环境中,不存在“离散”的物体,也没有计数的需求。
因此,水母文明几乎不可能发明出整数、计数等数学概念,更不可能发展出基于离散概念的算术与代数。阿蒂亚由此得出结论:“通过理想化和抽象物理世界中的那些基本要素,人类创造了数学。”数学并非独立于人类认知的客观存在,而是人类根据自身的生存体验,对物理世界进行理想化、抽象化处理后所构建的思维体系。
语言学家乔治·莱考夫(George Lakoff)与心理学家拉斐尔·努涅斯(Rafael Núñez)从认知科学的角度,进一步佐证了“数学是发明”的观点。
二人在合著的《数学从哪里来》一书中,通过对人类认知过程的深入研究,提出了“具身认知”的数学观:数学并非纯粹的理性产物,而是源于人类的身体体验与大脑的认知结构。莱考夫与努涅斯认为,人类的数学思维能力并非与生俱来的“天赋”,而是在长期的进化过程中,为了适应环境、解决生存问题而逐渐发展出来的。例如,人类对“数量”的感知,源于对身体部位的计数(如用手指计数);对“空间”的认知,源于对自身与周围物体位置关系的体验;对“运算”的理解,源于对物理动作的抽象(如将“合并”的动作抽象为“加法”,将“分离”的动作抽象为“减法”)。
莱考夫与努涅斯强调,所有的数学概念与理论,都是人类通过“隐喻”这一认知工具,从具体的身体体验向抽象的思维领域延伸的结果。例如,“直线”的概念,是对“两点之间最短路径”这一物理现象的抽象;“函数”的概念,是对“一个量随另一个量变化”这一关系的抽象;“无穷”的概念,则是对“不断延伸、没有尽头”这一身体体验的隐喻延伸。在他们看来,数学本质上是一种“隐喻性的建构”,是人类心智的创造性发明,而非对客观规律的发现。

“数学是发明”的观点,还引发了一个极具争议的衍生问题:如果数学是人类的主观发明,那么它是否具有普遍性?假如外星文明真的存在,它们所发明的数学体系会与人类的数学体系相同吗?
著名天文学家卡尔·萨根(Carl Sagan)曾对此持乐观态度,他在《宇宙》一书中提出,质数是宇宙间普遍存在的数学规律,任何智能文明都有可能发现质数的存在。萨根认为,如果人类向宇宙中发射包含质数序列的无线电信号,外星文明接收到后,必然能够识别出这是智能生命的产物——因为任何自然的物理过程都不可能产生如此规整的质数序列。但这一观点显然忽略了数学的“发明属性”:如果外星文明的生存环境与认知结构与人类截然不同,它们可能根本不会发明出“质数”这一数学概念,自然也就无法识别质数序列所蕴含的信息。
数学物理学家史蒂芬·沃尔夫拉姆(Stephen Wolfram)则提出了更为激进的观点。他在《一门新科学》一书中指出,人类所构建的数学体系,只是众多可能的“数学范式”中的一种。沃尔夫拉姆认为,人类之所以选择基于数学公式的法则来描述自然,是因为这种范式符合人类的认知习惯,但这并不意味着它是唯一的、普遍的范式。事实上,人类完全可以使用其他类型的法则(如简单的计算机程序)来描述自然现象,而这些法则所对应的“数学体系”,可能与我们目前所使用的数学体系截然不同。在沃尔夫拉姆看来,人类的数学只是“数学之树”上盛开的一朵“花朵”,而外星文明可能会基于自身的认知结构,发明出完全不同的“数学花朵”。
还有一些学者从语言与大脑功能的角度,探讨了数学的发明属性。部分分子生物学家与认知学家通过对大脑功能的研究发现,数学能力与语言能力有着密切的关联,二者在大脑的认知加工过程中存在诸多相似之处。换句话说,数学与语言一样,都是人类文明的产物,是人类用于交流与理解世界的工具。法国神经系统学家让-皮埃尔·尚热(Jean-Pierre Changeux)就曾指出:“对我而言,公理化方法(欧几里得几何学就建立在几条公理之上)就是与使用大脑相关的脑功能的表现。”在他看来,欧几里得几何学的公理体系,并非对客观空间规律的绝对反映,而是人类大脑为了简化对空间的认知、构建有序的思维体系而发明的规则。
不过,这一观点也面临着一个难以回避的疑问:如果数学与语言都是人类的发明,为何孩子学习语言时相对轻松,而学习数学时却常常倍感吃力?对此,认知学家给出的解释是:语言的发明是为了满足日常交流的需求,其规则与人类的日常体验紧密相关,因此更容易被大脑接受;而数学的发明则是为了满足抽象思维与逻辑推理的需求,其概念与规则往往远离日常体验,需要大脑进行更复杂的认知加工,因此学习起来难度更大。这一差异恰恰说明,数学是人类在语言基础上,进一步抽象、创造出来的更高级的思维工具,其发明属性更为显著。
黄金分割率:数学发明与发现的双重例证
要破解“数学是发明还是发现”的争议,最具说服力的方式便是从具体的数学案例出发,分析其背后所蕴含的发明与发现的双重属性。在众多数学概念中,欧几里得提出的“黄金分割率”无疑是最理想的例证。黄金分割率不仅是古希腊数学的重要成果,更在历史发展过程中被赋予了丰富的文化内涵,其形成过程清晰地展现了数学的发明性与发现性的统一。
在欧几里得的不朽名著《几何原本》中,黄金分割率有着明确的定义。

《几何原本》第6卷中记载了黄金分割率的线段分割定义:将一条线段AB分为两段AC与CB(其中AC>CB),如果较长线段AC与较短线段CB的比值,等于整条线段AB与较长线段AC的比值(即AC/CB = AB/AC),那么这种分割方式就被称为“中末比”。而在《几何原本》第2卷中,欧几里得还从面积的角度,对黄金分割率进行了补充定义。这一比例在19世纪被正式命名为“黄金分割率”,其数值约为1.618(准确表达式为(1+√5)/2)。
或许有人会疑问:世界上存在无数种分割线段的方式,欧几里得为何偏偏要挑选出这种分割方式,并专门为其下定义、进行系统研究?要回答这个问题,就必须回到古希腊的文化背景中,从毕达哥拉斯学派与柏拉图学派的神秘主义思想中寻找答案。毕达哥拉斯学派是古希腊最早的数学学派,他们痴迷于数的研究,认为数是宇宙的本质,一切事物都可以用数来解释。在毕达哥拉斯学派的认知中,数不仅具有数学意义,还被赋予了道德、性别等文化属性——他们认为奇数代表男性、善良与完美,偶数代表女性、邪恶与缺陷。
在众多数字中,毕达哥拉斯学派对数字5有着特殊的偏爱。他们认为,5是第一个奇数(3)与第一个偶数(2)的和,象征着男性与女性的结合,因此是爱情与婚姻的化身。而五角星作为由5条线段组成的图形,被毕达哥拉斯学派视为兄弟情谊的象征,其内部就蕴含着黄金分割率的比例关系。这是黄金分割率第一次出现在人类历史的记载中。如果我们仔细测量正五角星中任意一个三角形的长边与底边的比值,就会发现其比值恰好等于黄金分割率;同时,正五角星内部所包含的正五边形,其对角线与边长的比值也等于黄金分割率。更重要的是,在古希腊时期,人们已经掌握了用直尺和圆规绘制正五角星的方法,而这一绘制过程的核心步骤,就是将一条线段按照黄金分割率进行分割。
在毕达哥拉斯之后,柏拉图进一步赋予了黄金分割率神秘的宇宙学内涵。古希腊人普遍认为,宇宙由土、火、空气、水四种基本元素构成,而柏拉图在其对话录《蒂迈欧篇》中,提出了“柏拉图多面体”的理论,用五种正多面体来解释宇宙的结构。这五种正多面体分别是正四面体、立方体(正六面体)、正八面体、正十二面体和正二十面体,它们是仅有的五种各面均为全等正多边形、且所有顶点都在同一球面上的凸多面体。柏拉图将这五种多面体与宇宙的四种基本元素对应起来:正四面体对应火,立方体对应土,正八面体对应空气,正二十面体对应水。
对于剩下的正十二面体,柏拉图在《蒂迈欧篇》中写道:“对于剩下的第5种复合图形,上帝用它来代表全部,并给它绣上精美的图案。”也就是说,在柏拉图眼中,正十二面体是整个宇宙的象征。值得注意的是,正十二面体的每一个面都是正五边形,而正五边形的对角线与边长的比值恰好是黄金分割率;同时,正十二面体的体积、表面积等几何参数,都可以用黄金分割率的表达式来精确计算。不仅如此,与正十二面体有着密切关联的正二十面体,其几何结构中也处处蕴含着黄金分割率的身影。柏拉图通过将正十二面体与宇宙相联系,进一步提升了黄金分割率的文化地位,使其成为古希腊数学与哲学思想的重要符号。
从历史发展的角度来看,黄金分割率的形成过程清晰地展现了数学的发明属性。首先,毕达哥拉斯学派在观察正五角星的几何结构时,发现了这一特殊的比例关系,但他们并没有将其抽象为独立的数学概念;直到欧几里得在《几何原本》中,通过严格的定义将这一比例关系从具体的几何图形中抽象出来,并命名为“中末比”,黄金分割率才成为一个正式的数学概念。这一过程并非对客观规律的简单发现,而是人类心智的创造性建构——欧几里得凭借自己的数学智慧,从无数种线段分割比例中挑选出这一具有特殊文化内涵与几何属性的比例,对其进行系统的分析与研究,并将其纳入到欧氏几何学的理论体系中。正是这种创造性的抽象与建构,使得黄金分割率从一个偶然发现的几何现象,成为了一个具有广泛影响力的数学概念。
更能体现黄金分割率发明属性的,是其文化差异性。通过对不同文明数学文献的研究发现,古代中国与古印度的数学家们,尽管在数学领域取得了辉煌的成就(如古代中国的《九章算术》、古印度的三角学研究),但他们始终没有发明出“黄金分割率”这一独立的数学概念。在古代中国的数学文献中,虽然有关于线段分割、几何图形的研究,但从未对黄金分割率进行过明确的定义与系统的探讨;古印度的数学家在研究三角学定理时,虽然曾隐约涉及到黄金分割率的比例关系,但也没有将其抽象为一个独立的数学概念。这一现象充分说明,黄金分割率并非宇宙间普遍存在的、等待被发现的客观规律——如果它是客观存在的,那么不同文明的数学家都应该能够“发现”它;恰恰相反,它是古希腊数学家基于自身的文化背景与数学需求,所发明的一个特殊数学概念。
与此同时,黄金分割率的发展过程也展现了数学的发现属性。一旦欧几里得发明了黄金分割率的概念,并将其纳入欧氏几何学的体系中,就会发现一系列不依赖于人类主观意志的客观规律。例如,黄金分割率的数值是一个无理数,其准确表达式为(1+√5)/2,这一数值是固定不变的,无论人类是否计算出它的具体数值,它都客观存在;再如,黄金分割率与斐波那契数列之间存在着密切的关联——斐波那契数列是指从第三项开始,每一项都等于前两项之和的数列(1,1,2,3,5,8,13,21,...),如果用斐波那契数列中的任意一项除以它前面的一项,其结果会随着数列的递增而逐渐趋近于黄金分割率。这一关联并非人类的主观创造,而是黄金分割率与斐波那契数列各自的数学属性所决定的客观规律,是人类在研究过程中“发现”的。
更令人惊叹的是,黄金分割率不仅存在于数学理论之中,还被“发现”于自然界的诸多现象中。现代科学研究发现,在植物的叶序排列中,黄金分割率有着广泛的应用——许多植物的叶片在茎干上的排列方式,遵循着黄金分割率的比例,这种排列方式能够最大限度地提高叶片接收阳光的效率。
例如,向日葵花盘上的种子排列成螺旋状,其螺旋线的数量往往是斐波那契数列中的数字,而螺旋线之间的夹角则接近黄金分割率;松果、菠萝等植物的鳞片排列,也遵循着类似的规律。此外,在部分铝合金晶体的结构中,科学家也发现了黄金分割率的身影。这些自然现象中的黄金分割率,并非人类发明的结果,而是自然界在长期进化过程中形成的客观规律,人类的任务只是通过数学研究,发现这些规律与黄金分割率之间的关联。



























热门跟贴