在编程教育越来越普及的今天,许多青少年在小学阶段就开始接触NOI(全国青少年信息学奥林匹克竞赛)相关的知识点。编程基础、算法入门和基本的数据结构等知识为他们的学习之路打下了坚实的基础。然而,尽管小学阶段的学习看似已经覆盖了信息学的诸多方面,但实际上这只是冰山一角。
初高中阶段,信息学竞赛的学习远不止于知识点的掌握,更在于深度理解、题型拓展与解题策略的培养。小学时积累的知识和经验,为这一阶段的深入学习提供了良好的起点,但真正的挑战和机遇才刚刚开始。
小学到初高中的跨度对比
1、学习规划与目标对比
小学阶段的信息学学习着重于培养孩子的逻辑思维能力和数理基础,旨在为未来的深入学习打下坚实基础。
而进入初、高中阶段,学习重心则转向了对算法和数据结构的深度理解与应用能力的提升,在初中阶段,孩子们可以通过参与信息学竞赛来展现自己的科技特长,增强自身竞争力,到了高中阶段,还可以通过强基计划等途径为高考增添更多机会。这两个阶段的学习共同推动孩子在信息学领域实现从基础到精通的质的飞跃。

2、知识点回顾与对比
小学阶段,孩子们可能已经从直观的冒泡排序过渡到了稍微复杂的归并排序和快速排序。这些基础排序算法的学习,不仅让他们理解了算法的基本概念,还初步锻炼了逻辑思维和问题解决能力。进入初、高中,这些知识将进一步深化。归并排序和快速排序的优化、稳定与非稳定排序的理解、以及它们在不同场景下的应用,都将成为学习的重点。


3、深度与广度的双重提升
初、高中的信息学学习,不仅仅是知识点数量的增加,更是对每个知识点的深度挖掘。数据结构与算法的优化技巧,如图论中的最短路径算法(Dijkstra、Floyd-Warshall)、最小生成树算法(Kruskal、Prim),以及动态规划的更深入应用,比如状态压缩、树形DP,都是对小学阶段知识的极大拓展。
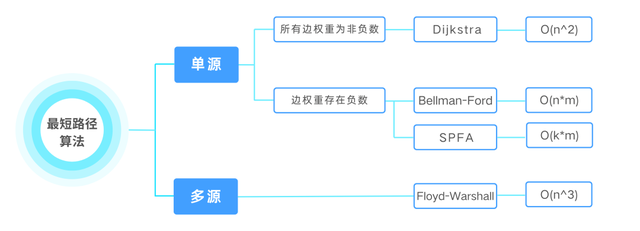
这些算法的掌握,不仅需要理解其背后的数理逻辑,更需要在实践中不断尝试、调整和优化,以达到最佳性能。小学初次接触的学习为这些深入探索打下了坚实的基础,而随着年龄的增长和思维的成熟,学生们能够更好地融合和应用这些知识。

面对多样化的题型与挑战
1、题型拓展
初、高中信息学竞赛的题型更加多样化,涵盖了字符串处理、图论、组合数学、动态规划等多个领域。例如,字符串处理中的KMP算法、后缀数组,图论中的网络流、二分图匹配,这些题型不仅考察算法的应用,更考验学生的抽象思维和问题解决能力。
通过经典案例,如“最长公共子串”、“最小费用最大流”等,学生们可以直观感受到难度提升之处,以及解决这些问题所需的新知识和解题思维。


2、题目难度的层次递进
题目难度的增加,体现在多个方面:
数据量显著增大,要求算法具有更高的效率
时间复杂度要求更加严格,需要精细的时间复杂度分析
问题抽象层次加深,需要从复杂的问题描述中提炼出要点
解决这些难题,不仅需要扎实的基础知识,更需要良好的问题分析和解决策略,如分而治之、贪心策略、动态规划等。
3、心理素质的培养
竞赛环境下,良好的心理素质同样重要。面对高压和挑战,学生们需要学会压力管理,保持冷静和专注。通过模拟竞赛、团队讨论、心理调适训练等方式,增强自信心,学会在失败中寻找成长的机会,保持积极的学习态度。

对“算法优化”要求的深入
在小学阶段,孩子们可能更多地关注于知识点的应用和实践。然而,随着竞赛难度的提高和算法学习的深入,算法优化是提升程序性能的关键手段。
初、高中阶段的选手大多投身于编程竞赛之中,这就要求选手们需要根据题目要求选择合适的算法,并进行优化,以取得高分。而这些技巧的学习和应用,需要理论与实践相结合,也都是初、高中选手不断在实践中需要摸索和总结的地方。
具体而言,比如在时间复杂度优化方面,初、高中阶段的选手需要注重减少冗余操作,避免不必要的计算和比较,从而降低算法的执行时间。同时,使用更高效的数据结构也是优化时间复杂度的重要手段。
例如,哈希表在查找操作中的性能通常优于链表。此外,优化算法逻辑本身也是降低时间复杂度的有效途径,比如,使用归并排序或快速排序等高级排序算法代替冒泡排序等简单算法,可以显著提高排序效率。

数组能够方便定位到任何数据项,但扩展性较差;链表则无法提供快捷的数据项定位,但插入和删除任意一个数据项都很简单;通过结合数组和链表的优点,哈希表能够达到较好的扩展性和较高的访问效率
在空间复杂度优化方面,选手需要关注减少内存占用,通过优化算法中的内存分配和释放策略,避免不必要的内存浪费。

结语
即使孩子们在小学阶段已经接触并学习了NOI难度的相关知识点,并且学到了很高的级别,到了初、高中阶段依然有着广阔的学习空间和深度。
初、高中的信息学学习不仅是对小学阶段所学知识的深化和拓展,更是对孩子逻辑思维、问题解决能力和算法设计与优化能力的全面提升。因此,家长们应该鼓励孩子们继续保持对信息学的热爱和学习热情,不断探索和挑战自己,在信息学的道路上越走越远。


























热门跟贴